Plano Cartesiano
Plano Cartesiano
Plano Cartesiano foi criado pelo matemático René Descartes. Como ele associava a geometria à álgebra, esta foi a forma que ele criou para representar graficamente expressões algébricas.
A sua utilização mais simples é a de representarmos graficamente a localização de pontos em um determinado plano. Através dele também podemos representar um segmento de reta ou um triângulo, por exemplo.
O plano cartesiano é composto de duas retas perpendiculares e orientadas, uma horizontal e outra vertical.
Damos no nome de eixo x ou eixo das abscissas à reta horizontal. À vertical denominamos de eixo y ou eixo das ordenadas.
A orientação positiva das retas é representa por uma seta como podemos ver na figura mais abaixo.
Representação de Pontos no Plano Cartesiano
A representação de pontos neste plano é feita através de pares ordenados, onde o primeiro número se refere àabscissa e o segundo a ordenada.
O ponto P1(3, 2) tem abscissa 3 e ordenada 2, no qual o símbolo (3, 2) representa um par ordenado. O pontoP2(2, 3) tem abscissa 2 e ordenada 3. É importante frisarmos que os pontos P1 e P2 são pontos distintos, poisem um par ordenado a ordem dos números é relevante.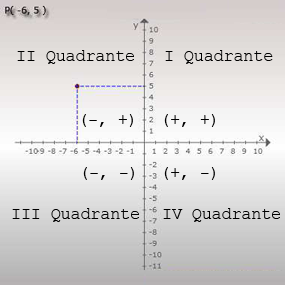
Dois pares ordenados (a, b) e (c, d) são iguais se e somente sea = c e b = d.
Na figura ao lado vemos a representação do ponto P(-6, 5).
Ao ponto localizado no cruzamento de ambos os eixos damos o nome de origem do sistema de coordenadas cartesianas, representado por O(0, 0).
Quadrantes do Plano Cartesiano
Vemos nesta figura que o eixo x e o eixo y dividem o plano em quatro regiões. A região do canto superior direito é o primeiro quadrante, a região à sua esquerda, do outro lado do eixo y é osegundo quadrante. Abaixo deste temos o terceiro quadrante e à sua direita, ou seja, abaixo do primeiro temos o quarto quadrante.
Os quadrantes são dispostos em sentido anti-horário.
Sinal da Abscissa e da Ordenada de um Ponto
Todos os pontos no primeiro quadrante possuem abscissa e ordenada positivas. Exemplo: P1(3, 5).
No segundo quadrantes todos os pontos possuem abscissa negativa e ordenada positiva. Exemplo: P2(-4, 2).
Todos os pontos no terceiro quadrante possuem abscissa e ordenada negativas. Exemplo: P3(-7, -1).
No quarto quadrante todos os pontos possuem abscissa positiva e ordenada negativa. Exemplo: P2(8, -3).
Exercícios Práticos
Embora os conceitos aqui expostos sejam bastante simples, é bom que você pratique um pouco para verificar se os assimilou de fato.
Abaixo lhe propomos algumas tarefas que você deve realizar.
Na figura abaixo, ou melhor, dizendo, no aplicativo abaixo, ao movimentar o mouse serão exibidas no topo algumas informações. No canto esquerdo serão mostradas as coordenadas do ponto onde se localiza o mouse, na forma de fracionária, no canto direito a mesma representação é feita na forma decimal. No centro temos o quadrante onde se localiza o ponto.
O mouse se movimenta de décimo em décimo.
Para começar basta que você clique na figura e movimente o mouse para o ponto em questão.
Quando encontrar o ponto, clique novamente para bloquear a movimentação. Para localizar um outro ponto, clique outra vez.
Vamos lá!
Localize os Pontos:
 P(-6, 5)
P(-6, 5)
 Origem do sistema
Origem do sistema
 P(3, 3/5)
P(3, 3/5)
 P(41/2, -7)
P(41/2, -7)
 P(-5,5, -3,3)
P(-5,5, -3,3)
Em Quais Quadrantes se Encontram os Pontos?
 P(3, 3)
P(3, 3)
 P(-3, -3)
P(-3, -3)
 P(-3, 3)
P(-3, 3)
 P(3, -3)
P(3, -3)
 P(0, 0)
P(0, 0)
 P(-1, 0)
P(-1, 0)
 P(0, -2)
P(0, -2)
Note que os três últimos pontos não se encontram em nenhum quadrante, pois eles estão localizados sobre o eixo x, o eixo y, ou sobre a origem do sistema.
Aqui vamos explicar mais para vocês :
Exercícios sobre Função de 1º Grau
Teste os seus conhecimentos: Faça exercícios sobre Função de 1º Grau e veja a resolução comentada.
Questão 1
(U. F. Viçosa-MG)
Uma função f é dada por f(x) = ax + b, em que a e b são números reais. Se f(–1) = 3 e f(1) = –1, determine o valor de f(3).
Resposta Questão 1
f(x) = ax + b
f(–1) = 3
f(–1) = a * (–1) + b
3 = – a + b
f(1) = –1
f(1) = a * 1 + b
–1 = a + b
Sistema de equações

Isolando b na 1ª equação
–a + b = 3
b = 3 + a
Substituindo o valor de b na 2ª equação
a + b = –1
a + 3 + a = –1
2a = –1 – 3
2a = –4
a = – 2
Substituindo o valor de a na 1ª equação
b = 3 + a
b = 3 – 2
b = 1
A função será dada pela expressão f(x) = – 2x + 1. O valor f(3) será igual a:
f(3) = –2 * 3 + 1
f(3) = – 6 + 1
f(3) = – 5
O valor de f(3) na função f(x) = – 2x + 1 é igual a –5.
Questão 2
(PUC-BH)
A função linear R(t) = at + b expressa o rendimento R, em milhares de reais, de certa aplicação. O tempo t é contado em meses, R(1) = –1 e R(2) = 1. Nessas condições, determine o rendimento obtido nessa aplicação, em quatro meses.
Resposta Questão 2
R(1) = –1
R(1) = a * 1 + b
–1 = a + b
a + b = –1
R(2) = 1
R(2) = a * 2 + b
1 = 2a + b
2a + b = 1
Sistema de equações

Isolando b na 1ª equação
a + b = –1
b = –1 – a
Substituindo o valor de b na 2ª equação
2a + b = 1
2a + (–1 – a) = 1
2a – 1 – a = 1
a = 1 + 1
a = 2
Substituindo o valor de a na 1ª equação
b = – 1 – a
b = –1 – 2
b = –3
A função será dada pela seguinte lei de formação: R(t) = 2t – 3.
Fazendo f(4), temos:
R(t) = 2 * 4 – 3
R(t) = 8 – 3
R(t) = 5
O rendimento obtido nessa aplicação será de R$ 5 000,00.
